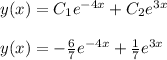Question

Section 5.2 Problem 18:

Solve the initial value problem and graph the solution.

`y'' + 7y' + 12y = 0`

`y(0) = - 1`

`y'(0) = 0`
​

Answer 1

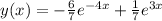`y(x)=-(6)/(7)e^(-4x)+(1)/(7)e^(3x)` (See attached graph)

Explanation:

Given Second-Order Homogeneous Differential Equation

`y''+7y'+12y=0,y(0)=-1,y'(0)=0`

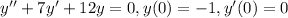
Use Auxiliary Equation

`m^2+7m+12=0\\\\(m+4)(m+3)=0\\\\m=-4,\: m=3`

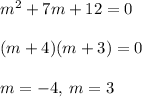
General Solution for Distinct Real Roots

`y(x)=C_1e^(m_1x)+C_2e^(m_2x)\\\\y(x)=C_1e^(-4x)+C_2e^(3x)`

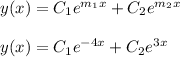
Take the derivative of y(x)

`y'(x)=-4C_1e^(-4x)+3C_2e^(3x)`

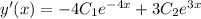
Create a system of equations given initial conditions

`y(x)=C_1e^(-4x)+C_2e^(3x)\\\\y(0)=C_1e^(-4(0))+C_2e^(3(0))=-1\\\\C_1+C_2=-1`

`y'(x)=-4C_1e^(-4x)+3C_2e^(3x)\\\\y'(0)=-4C_1e^(-4(0))+3C_2e^(3(0))=0\\\\-4C_1+3C_2=0`

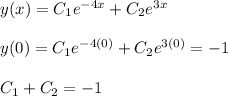
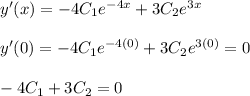
Solve the system of equations

`\left \{ {{C_1+C_2=-1} \atop {-4C_1+3C_2=0}} \right.\\\\\left \{ {{4C_1+4C_2=-1} \atop {-4C_1+3C_2=0}} \right.\\\\7C_2=-1\\\\C_2=-(1)/(7)`

`C_1+C_2=-1\\\\C_1-(1)/(7)=-1\\ \\C_1=-(6)/(7)`

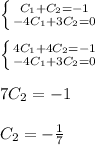
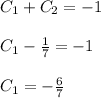
Final Solution

`y(x)=C_1e^(-4x)+C_2e^(3x)\\\\y(x)=-(6)/(7)e^(-4x)+(1)/(7)e^(3x)`