Answer;
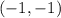
Explanation;
Here, we want to get the solution a pair of linear equation which we are to solve simultaneously by the graphical method
We need to plot the graphs of these two lines; The point at which the lines meet will represent the solution to the system of linear equations
The general equation of a straight line is;
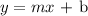
where m is the slope and b is the y-intercept
To plot the lines, we need the x-intercepts and the y-intercepts
This refer to the point at which the line touches the x and y axes respectively
Let us take the lines one after the other;

The y-intercept here is -4; so the point is (0,-4)
To get the x-intercept value, we simply set y to zero and get the value of x
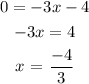
So the x-intercept is (-4/3,0)
To plot the line; we simply join (0,-4) and (-4/3,0)
For the second line;
We have the y-intercept as -2
So the point is (0,-2)
To get the x-intercept, we simply set y to 0 and solve for x
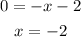
So, the x-intercept point is (-2,0)
We can now join (0,-2) and (-2,0) to represent the second line
Proceeding, we get the lines on the cartesian grid
This is shown in the attachment below;
As we can see from the plot, the lines touch at the point (-1,-1) and that represents the solution to the equation