Let's set x=number of times you go Go Carting and y=number of times doing Laser Tag.
The first condition is: you spend $20 per Go Cart ride, then the total amount you spend on Go cart can be represented as 20x, also you spend $10 per game of Laser Tag, the money you spend on this is 10y.
You want to spend no more than $180 on Fun center activities this year, thus, the inequality is:
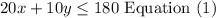
The second condition is: you want your number of times doing Laser Tag to be at least twice the number of times you go Go Carting, thus the second inequality is:
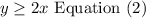
The third condition is: you only want to do Go Cart like 4 times at the most. The third inequality is then:

To graph the first inequality, let's find two points on the line.
Start with x=0, replace this value into equation (1) and solve for y:

Thus, the first point is (0,18)
Now, when y=0, the x-value is:
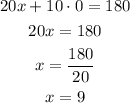
The second point is (9,0).
To graph the inequality, joint these two points and this is the line which represents the inequality:
Let's do the same procedure for equation 2.
When x=0:
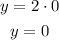
Thus, the first point is (0,0).
Now, when x=4:
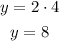
The second point is (4,8). Join the points and graph the inequality:
And finally, equation 3 is a vertical line at x=4, and the graph which represents the inequality is:
The graph which represents how many go Carts and Laser Tags you can buy is the result of overlapping the 3 graphs above, and it looks like this:
As x and y can't be negative, then the solution to the system is into the figure formed by the points (0,0) , (4,8), (4,10) and (0,18).
b. One possible solution to the system of inequalities is (4,8), it means you can go 4 times to Go Carting, and 8 times to do Laser Tag and you will spend no more than $180, the number of times you do Laser Tag is at least twice the number you go Go Carting and, you do Go Cart at the most 4 times.