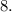Question

Brandon typically takes 2 less hours than Maria to assemble a bicycle if each works alone. Brandon and Maria worked together to assemble a bicycle for 3 hours, and then Maria finished the job without Brandon after an additional 1 hour. How long would it have taken Maria to assemble the bicycle alone? Do not include the units in your answer.

Answer 1

Let x be the rate at which Maria can assemble a bicycle, and y the rate at which Brandon can assemble a bicycle, then we can set the following equation:

`3y+4x=1.`

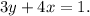
Now, we know that Maria takes 2 hours more to assemble a bicycle on her own, therefore:

`(1)/(x)-2=(1)/(y)\text{.}`

Solving the above equation, for y, we get:

`\begin{gathered} (1-2x)/(x)=(1)/(y), \\ y=(x)/(1-2x)\text{.} \end{gathered}`

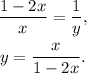
Substituting the above result in the first equation, we get:

`3((x)/(1-2x))+4x=1.`

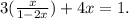
Solving the above equation for x, we get:

`\begin{gathered} (3x)/(1-2x)+4x=1, \\ 3x+4x(1-2x)=1-2x, \\ 3x+4x-8x^2=1-2x, \\ -8x^2+7x=1-2x, \\ -8x^2+9x-1=0. \end{gathered}`

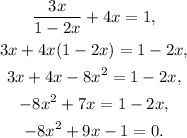
Using the quadratic formula, we get:

`\begin{gathered} x_1=1, \\ x_2=(1)/(8)\text{.} \end{gathered}`

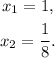
The first solution for x has no meaning in this context because that would imply that Maria can assemble the bicycle in 1 hour and that Brandon can assemble one in 2 hours less than that, therefore, Maria can assemble 1 bicycle in 8 hours.

Answer:

`8.`