Answer:
![y(x)=e^(-3x)[C_1cos(2x)+C_2sin(2x)]](https://img.qammunity.org/2023/formulas/mathematics/college/vw2gdy6u5i0eux6ysa0ynw222kjifll3zi.png)
Explanation:
To solve a second-order homogeneous differential equation, we need to substitute each term with the auxiliary equation
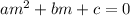 where the values of
where the values of
 are the roots:
are the roots:
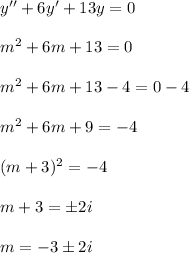
Since the values of
 are complex conjuage roots, then the general solution is
are complex conjuage roots, then the general solution is
![y(x)=e^(\alpha x)[C_1cos(\beta x)+C_2sin(\beta x)]](https://img.qammunity.org/2023/formulas/mathematics/college/owjcnyjsusa1zucdl5hddhyzontd845mq0.png) where
where
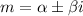 .
.
Thus, the general solution for our given differential equation is
![y(x)=e^(-3x)[C_1cos(2x)+C_2sin(2x)]](https://img.qammunity.org/2023/formulas/mathematics/college/vw2gdy6u5i0eux6ysa0ynw222kjifll3zi.png) .
.