Question

5. What is the length of the line segment? Express your answer as an exact value an to one decimal place. B. YA 6- А 2- 6 x

Answer 1

`AB=3.6`

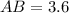
1) Let's locate the endpoints of that line segment on the Plane.

2) Point A ( (1,4) and Point B (4,6) so let's find the length of that segment using the distance formula, derived from the Pythagorean Theorem

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \end{gathered}`

So now, let's plug those coordinates into that.

2.2)

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d=\sqrt[]{(4_{}-1_{})^2+(6-4_{})^2} \\ d=\sqrt[]{13}\approx3.6 \end{gathered}`

Notice that we could have found this length had we used the Pythagorean Theorem since this is a small triangle.

3) Thus, the answer is 3.6