Question

what is the perimeter of an equilateral triangle with a height of 6 feet?A.
`2 √(3)`B.
`4 √(3)`C.
`6 √(3)`D.
`12 √(3)`

Answer 1

To solve this question, first, we will have a pictorial representation of the given problem.

An equilateral triangle has all its' sides equal.

So we have made the length of one side x.

To get the perimeter of the triangle, we will sum up the length of the 3 sides together.

To solve for the length of the triangle, we will analyze a right-angle part from the full triangle, the image is drawn below.

To solve for x (a side of the equilateral triangle), we will use the Pythagoras theorem:

`\begin{gathered} \text{hypotenuse}^2=adajcent^2+opposite^2 \\ \text{hypotenuse side =x} \\ \text{adjacent side = }(x)/(2) \\ \text{opposite side = 6} \end{gathered}`
`\begin{gathered} x^2=((x)/(2))^2+6^2 \\ x^2-(x^2)/(4)=36 \\ (4x^2-x^2)/(4)=36 \\ (3x^2)/(4)=36 \\ \end{gathered}`

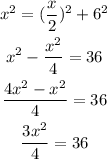
Cross multiply, we will have:

`\begin{gathered} 3x^2=36*4 \\ 3x^2=144 \\ x^2=(144)/(3) \end{gathered}`
`\begin{gathered} x^2=48 \\ x=\sqrt[]{48} \\ x=4\sqrt[]{3} \end{gathered}`

So now we have gotten the length of a side of the equilateral triangle, the perimeter will be:

`\begin{gathered} \text{Perimeter}=3*\text{ (x)} \\ =3*(4\sqrt[]{3)} \\ =12\sqrt[]{3} \\ \text{The correct answer therefore is option D.} \end{gathered}`