Recall that the sum of all probabilities should up to 1. Let x be the probability of 11-14 babies/day.
Then we have the equation
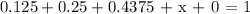
which is equivalent to the equation
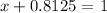
So by subtracting 0.8125 on both sides we get

So the probability of having 11-14 babies/day is 0.1875.
Now, to calculate the probability having at least 7 babies, we simply add the probabilities of the events where we have more than 7 babies. That is, sum 7-10 and 11-14 probabilities, which is

which is close to 63% of the time