Question

Determine whether the following function has a maximum, a minimum, or neither. If it has either a maximum or a minimum, find what that value is and where it occurs.Reduce all fractions to lowest terms.f(x) = - 4x^2 – 32x - 60

Answer 1

Given the function;

`f(x)=-4x^2-32x-60`

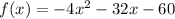
The maximum value of a function is the place where a function reaches its highest point, or vertex, on a graph. If a quadratic function has a negative "a" term, it will also have a maximum value.

Thus, the function has a maximum value.

Also;

`\begin{gathered} f^(\prime)(x)=(-4*2)x^(2-1)-(32*1)x^(1-1) \\ f^(\prime)(x)=-8x-32 \end{gathered}`

At maximum value, the derivative is zero. Thus;

`\begin{gathered} -8x-32=0 \\ -8x=32 \\ x=(32)/(-8) \\ x=-4 \end{gathered}`

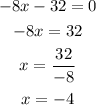
Then,