Let x be the miles you drive, now for the second company to be cheaper than the first one, we set the following inequality:

Solving for x we get:
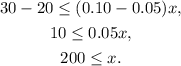
Therefore, for the second company to be cheaper the distance must be greater than 200 miles.
Answer: Above 200 miles.