The Solution:
Given the linear graphs in the Question section, we are required to find the system of equations represented in the given graphs (in the form: y=mx+b)
Step 1:
Pick two points on each of the given lines.
For the red line:
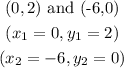
For the blue line:
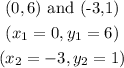
Step 2:
The formula for the equation of a line when two points are given is:
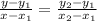
Step 3:
Substituting the appropriate values in the above formula.
For the red line:
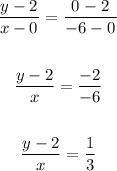
Cross multiplying, we get
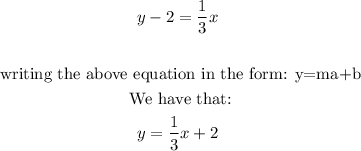
For the blue line:

Cross multiplying, we get

Therefore, the system of equations is:
