Question

Find the derivative with the formula: f’(a)=lim x-a f(x)-f(a)/x-aQuestion: f(x)=3x^2+x

Answer 1

Ok, so

Given the alternate definition of deritative:

`f^(\prime)(a)=\lim _(x\to a)((f(x)-f(a))/(x-a))`

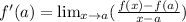
We want to find the deritative of the function:

`f(x)=3x^2+x`

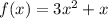
For this, we could start by replacing:

`f^(\prime)(a)=\lim _(x\to a)((3x^2+x-(3a^2+a))/(x-a))`

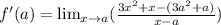
Now, we could distribute the sign outside the bracket:

`f^(\prime)(a)=\lim _(x\to a)((3x^2+x-(3a^2+a))/(x-a))=\lim _(x\to a)((3x^2+x-3a^2-a))/(x-a))`

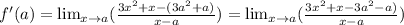
And, as you can see, this expression can be even more simplified if we factor. We have to ask for a way to eliminate the indeterminacy caused by the denominator:

`f^(\prime)(a)=\lim _(x\to a)((3(x^2-a^2)+(x-a))/(x-a))`

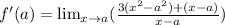
Now, remember that:

`x^2-a^2=(x+a)(x-a)`

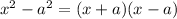
So, our expression will be:

`f^(\prime)(a)=\lim _(x\to a)((3(x^2-a^2)+(x-a))/(x-a))=\lim _(x\to a)(\frac{3(x-a^{})(x+a)+(x-a)}{x-a})`

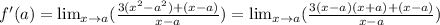
We could group some terms:

`f^(\prime)(a)=\lim _(x\to a)(\frac{3(x-a^{})(x+a)+(x-a)}{x-a})=\lim _(x\to a)(((x-a)\lbrack3(x+a)+1\rbrack)/(x-a))`

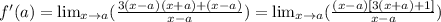
As you can see, the term (x-a) can be cancelled. And, our limit will be:

`\begin{gathered} f^(\prime)(a)=\lim _(x\to a)(3(x+a)+1)=(3(a+a)+1) \\ f^(\prime)(a)=3(2a)+1 \\ f^(\prime)(a)=6a+1 \end{gathered}`

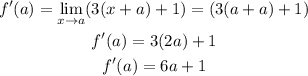
Therefore, f'(a)=6a+1