Answer:
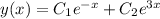
Explanation:
To solve a second-order homogeneous differential equation, we need to substitute each term with the auxiliary equation
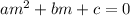 where the values of
where the values of
 are the roots:
are the roots:

Since the values of
 are distinct real roots, then the general solution is
are distinct real roots, then the general solution is
 .
.
Thus, the general solution for our given differential equation is
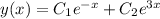 .
.