Question

Express your answer as a percentage rounded to the hundreths.

Answer 1

We have the formula to calculate the annual percentage yield that let us compare different investment or interest rates with different capitalization periods, transforming them in a consistent annual measure.

The formula is:

`\text{APY}=(1+(r)/(n))^n-1`

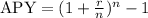
where r: nominal annual interest rate and n: subperiod of capitalization (number of capitalizations in a year).

In this case, with an interest rate of 3% (r=0.03) monthly compounded (n=12) we can calculate the APY as:

`\begin{gathered} \text{APY}=(1+(r)/(n))^n-1 \\ \text{APY}=(1+(0.03)/(12))^(12)-1 \\ \text{APY}=(1+0.0025)^(12)-1 \\ \text{APY}=1.0025^(12)-1 \\ \text{APY}\approx1.0304-1 \\ \text{APY}\approx0.0304 \\ \text{APY}\approx3.04\% \end{gathered}`

Answer: the APY for this investment is 3.04%.