Try each statement to figure out if it holds or not.
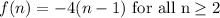
Try n=2, if the statement is true, then f(2) should be -4:
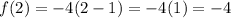
Try n=3, if the statement is true, then f(3) should be 0:
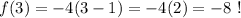
Therefore, the first statement is false.
Since the sequence is an arithmetic sequence, the first term is equal to -8 and the common difference of its terms is equal to 4, then the explicit rule for the sequence is:
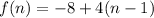
By trying different values of n you can convince yourself that this statement is true.
The tenth term is given by:
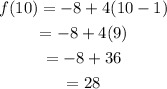
Therefore, the third statement is true.