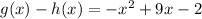We have the functions:
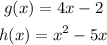
And we are asked for:

Which is to subtract the function h(x) from the function g(x).
The result of this subtraction is as follows:
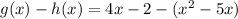
First, we multiply the minus sign outside the parenthesis by the numbers inside it:
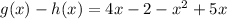
Now, we leave the term with the greatest exponent at the beginning and we add the like terms 4x and 5x which result in 9x.
So the simplified expression is as follows:
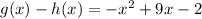
Answer: