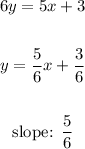The slopes of perpendicular lines are opposite reciprocals.
For the given function:
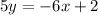
Solve y to identify the slope (y=mx+b, m is the slope)

The slope of the perpendicular line to the given function is 5/6. For the given options the equation with slope 5/6 is: B. 6y=5x+3