These are some Rules for the transformations of a function f(x):
a. If the function is shifted left "h" units, then:
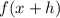
b. If the function is shifted right "h" units:
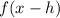
c. If the function is shifted up "h" units:

d. If it is shifted down "h" units:
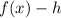
Notice that the red graph is this function:
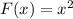
And both have the same shape, but the blue one is moved to the left 2 units. Therefore the equation of the blue graph is:
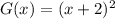
THE ANSWER IS OPTION A.