Define your variable:
Let x and y be two numbers.
What are you given?
We know that,
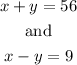
Create and solve a system.
The system is
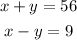
Explain your solution.
We can solve this systemn by elimination method. If we add both equation, we obtain

because y-y=0. Then, we have
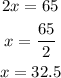
Now, we must substitute this value into the first equation. It yields,
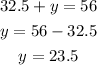
Therefore, the answer is x=32.5 and y=23.5