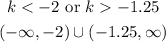Question

The equation (k+1)x² + 2(k+ 2)x= 3(k + 2) has real roots. Find the possible values of k.

Answer 1

In order to find the possible values of k, first let's put the equation in the standard form and equate it to zero:

`ax^2+bx+c=0`

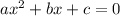
So we have:

`\begin{gathered} (k+1)x^2+2(k+2)x=3(k+2) \\ (k+1)x^2+2(k+2)x-3(k+2)=0 \\ a=k+1 \\ b=2(k+2) \\ c=-3(k+2) \end{gathered}`

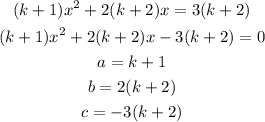
Now, let's calculate the discriminant:

`\begin{gathered} \Delta=b^2-4ac \\ \Delta=\lbrack2(k+2)\rbrack^2-4\cdot(k+1)\lbrack-3(k+2)\rbrack \\ \Delta=4(k^2+4k+4)+12(k+1)(k+2) \\ \Delta=4k^2+16k+16+12(k^2+3k+2) \\ \Delta=4k^2+16k+16+12k^2+36k+24 \\ \Delta=16k^2+52k+40 \end{gathered}`

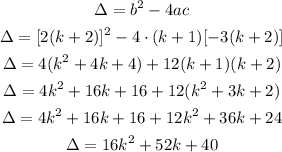
In order to have real roots, the value of the discriminant must be greater than zero, so we have:

`\begin{gathered} \Delta>0 \\ 16k^2+52k+40>0 \\ 4k^2+13k+10>0 \\ k=\frac{-13\pm\sqrt[]{13^2-4\cdot4\cdot10}}{2\cdot4} \\ k=\frac{-13\pm\sqrt[]{169-160}}{8} \\ k_1=(-13+3)/(8)=-(10)/(8)=-1.25 \\ k_2=(-13-3)/(8)=-2 \end{gathered}`

Since the coefficient of k² is positive, the discriminant will be positive for k < k2 or k > k1, that is:

`\begin{gathered} k<-2\text{ or }k>-1.25 \\ (-\infty,-2)\cup(-1.25,\infty) \end{gathered}`