0.965 mililΩ
Step-by-step explanationThe resistance of a metal rod depends on resistivy, length and temperature, it can fe found usign the formula
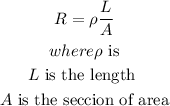
sp
Step 1
a) let
![\begin{gathered} \rho=2.8*10^(-8)m\text{ ^^^^2126} \\ L=2.39\text{ m} \\ d=0.4\text{ cm=0.4 cm\lparen}\frac{1m}{100\text{ cm}}\text{\rparen=0.0047 m} \end{gathered}]()
b) find the transversal area (A)
use the area of a circle
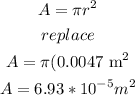
c) now, replace in the formula
![\begin{gathered} R=\rho(L)/(A) \\ R=2.8*10^(-8)m\text{ ^^^^2126*}\frac{2.39\text{ m}}{6.93*10^(-5)m^2} \\ R=0.00096565\text{ ^^^^2126} \end{gathered}]()
finally, to convert into milliOhms, Multiply by 1000
![\begin{gathered} R=0.000965365*1000\text{ m^^^^2126} \\ R=0.965\text{ m^^^^2126} \end{gathered}]()
therefore, the answer is
0.965 miliΩ
I hope this helps you