Question

The points (3, 2), (5, k) and (-k, 4) are collinear. Find the possiblevalues of k.

Answer 1

Since the points are collinear this means that the points are in the same line which in turns means that the slope between any two of the points given are equal. The slope between two points is given by:

`m=(y_2-y_1)/(x_2-x_1)`

Let's find the slope between the first and second point:

`\begin{gathered} m=(k-2)/(5-3) \\ m=(k-2)/(2) \end{gathered}`

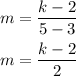
Now, let's find the slope between the first and third points:

`\begin{gathered} m=(4-2)/(-k-3) \\ m=-(2)/(k+3) \end{gathered}`

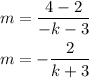
Since the slopes have to be equal, like we said above, we equate the expressions we found and solve the resulting equation for k:

`\begin{gathered} (k-2)/(2)=-(2)/(k+3) \\ (k-2)(k+3)=-4 \\ k^2+k-6=-4 \\ k^2+k-2=0 \\ (k+2)(k-1)=0 \\ \text{ then} \\ k+2=0 \\ k=-2 \\ \text{ or} \\ k-1=0 \\ k=1 \end{gathered}`

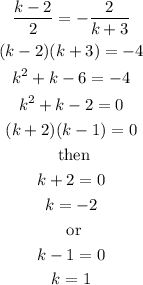
Therefore, the value of k for the points to be collinear is -2 or 1