Question

Two remote control cars with masses of 1.16 kilograms and 1.98 kilograms travel toward each other at speeds of 8.64 meters per second and 3.34 meters per second, respectively. The cars collide head-on, and the less massive car recoils with a speed of 2.16 meters per second.a. What is the final speed of the second car? Include units in your answer. More information. Hint: Pay attention to directions! Must be in 3 significant digits.

Answer 1

The initial momentum of the system can be expressed as,

`p_i=m_1u_1+m_{2_{}}u_2`

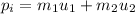
The final momentum of the system can be given as,

`p_f=m_1v_1+m_{2_{}}v_2`

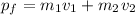
According to conservation of momentum,

`p_i=p_f`

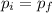
Plug in the known expressions,

`\begin{gathered} m_1u_1+m_2u_2=m_1v_1+m_2v_2 \\ m_2v_2=m_1u_1+m_2u_2-m_1v_1 \\ v_2=(m_1u_1+m_2u_2-m_1v_1)/(m_2) \end{gathered}`

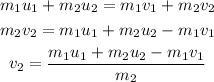
Initially, the second mass move towards the first mass therefore the initial speed of second mass will be taken as negative and the recoil velocity of first mass is also taken as negative.

Plug in the known values,

`\begin{gathered} v_2=\frac{(1.16\text{ kg)(8.64 m/s)+(1.98 kg)(-3.34 m/s)-(1.16 kg)(-2.16 m/s)}}{1.98\text{ kg}} \\ =\frac{10.02\text{ kgm/s-}6.61\text{ kgm/s+}2.51\text{ kgm/s}}{1.98\text{ kg}} \\ =\frac{5.92\text{ kgm/s}}{1.98\text{ kg}} \\ \approx2.99\text{ m/s} \end{gathered}`

Thus, the final velocity of second mass is 2.99 m/s.