Question

What type of triangle has side lengths 4, 4√15, and 16?A. not a triangleB. obtuseC. acuteD. right

Answer 1

There is a relationship between the length of the two shortest sides of a triangle and the length of its longest side.

If the triangle is not a right triangle, then the relationship is an inequality.

Just like in the Pythagorean Theorem, we call the short sides a and b and the long side c.

Hence, to know the type of triangle based on the sides given, we use the Pythagorean Inequality theorem.

Pythagorean inequality theorem states that if;

`\begin{gathered} c^2a^2+b^2,\text{ then it is an obtuse triangle.} \\ c^2=a^2+b^2,\text{ then it is a right triangle.} \end{gathered}`

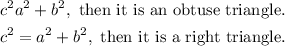
Given:

`\begin{gathered} a=4 \\ b=4\sqrt[]{15} \\ c=16 \end{gathered}`

To test and know which triangle it is,

`\begin{gathered} a^2=4^2=16 \\ b^2=(4\text{ }\sqrt[]{15})^2=240 \\ c^2=16^2=256 \\ a^2+b^2=16+240=256 \\ \text{Hence, } \\ a^2+b^2=c^2 \\ 256=256 \\ S\text{ ince } \\ a^2+b^2=c^2,\text{ then the triangle is a right triangle} \end{gathered}`

Therefore, the triangle is a right triangle.

The correct option is D.