we have the equation
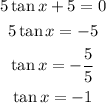
Remember that
tanx=1 -----> for x=45 degrees--------> x=pi/4
the value of the tangent is negative in the II quadrant and In the IV quadrant
In this problem
the domain for x is the interval [0,pi)
so
the quadrant of the solution is the second
the angle x is equal to
pi-pi/4=3pi/4
the solution for x=3pi/4