Question

Part 1: if (6^2)^x = 1, what is the value of x. Explain your answerPart 2: if (6^0)^x = 1, what is the value of x. Explain your answer

Answer 1

Part 1:

The given expression is

`(6^2)^x=1`

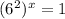
First, we multiply exponents

`6^(2x)=1`

Now, we take a square root on both sides

`\begin{gathered} \sqrt[]{6^(2x)}=\sqrt[]{1} \\ 6^x=1 \end{gathered}`

Then, we replace the following in the equation above

`1=6^0^{}`

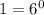
We replace this to have equal bases on both sides, which allows us to eliminate the powers

`\begin{gathered} 6^x=6^0 \\ x=0 \end{gathered}`

Therefore, the solution to this exponential equation is zero.

Part 2:

The given expression is

`(6^0)^x=1`

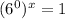
But, we know that

`6^0=1`

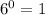
So,

`(1)^x=1`

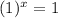
Then,

`x=1`

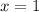
Because the unit power of one is equal to one.

Therefore, the solution to the second exponential function is 1.