10.
Consider the given function,
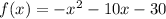
Solve for the critical points as,
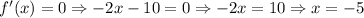
Thus, the given function has an extrema at point x= -5.
Apply the second derivative test,
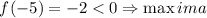
It is found that the function has a maxima at point x= -5.
Solve for the maximum value as,
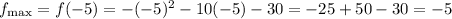
Thus, the maximum value of the function is -5.
Now, apply the leading coefficient test to find the end behavior of the function.
It is observed that the leading coefficient is negative, so according to the test, the value of the function approaches negative infinity as 'x' approaches infinity.
So the minimum value of the function tends to negative infinity,
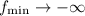
Now, solve for the ratio as,
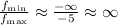
Thus, the ratio approaches infinity.