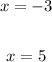Question

Identify all the rational zeros for f(x) = x3 + x2 - 21x – 45.

Answer 1

Given the following function:

`f\mleft(x\mright)=x^3+x^2-21x-45`

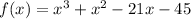
You need to apply the Rational Roots Test:

1. By definition, if the function has Whole coefficients, then its Rational roots have this form:

`(p)/(q)`

Where "p" represents of the factors of the Constant term and "q" represents all the factors of the Leading coefficient.

2. Identify that Leading coefficient. This is:

`a_n=1`

3. Identify that Constant term. In this case this is:

`a_0=_{}-45`

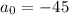
4. Find all the factors of the Leading coefficient (positive and negative):

`q=\pm1`

5. Find all the factors of the Constant term (positive and negative):

`p=\pm1,\pm3,\pm5,\pm9,\pm15,\pm45`

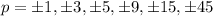
6. You can set up that:

`(p)/(q)=(\pm1,\pm3,\pm5,\pm9,\pm15,\pm45)/(\pm1)`

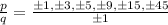
7. Find all the combinations

`\pm(p)/(q)`

You need to divide the numerator by each denominator. Since the denominator is 1:

`=\pm1,\pm3,\pm5,\pm9,\pm15,\pm45`

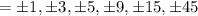
8. Since there are no duplicates, the next step is to substitute each value into the function. Remember that, If:

`P(a)=0`

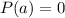
then "a" is a root of the polynomial.

Then:

`\begin{gathered} f(-1)=(-1)^3+(-1)^2-21(-1)-45=-24 \\ \\ \\ f(1)=(1)^3+(1)^2-21(1)-45=-64 \\ \\ \\ f(-3)=(-3)^3+(-3)^2-21(-3)-45=0\text{ (}-3\text{ is a root)} \\ \\ \\ f(3)=(3)^3+(3)^2-21(3)-45=-72 \\ \\ \\ f(-5)=(-5)^3+(-5)^2-21(-5)-45=-40 \\ \\ \\ f(5)=(5)^3+(5)^2-21(5)-45=0\text{ (}5\text{ is a root)} \\ \\ \\ f(-9)=(-9)^3+(-9)^2-21(-9)-45=-504 \\ \\ \\ f(9)=(9)^3+(9)^2-21(9)-45=576 \\ \\ \\ f(-15)=(-15)^3+(-15)^2-21(-15)-45=-2,880 \\ \\ \\ f(15)=(15)^3+(15)^2-21(15)-45=3,240 \\ \\ \\ f(-45)=(-45)^3+(-45)^2-21(-45)-45=-88,200 \\ \\ \\ f(45)=(45)^3+(45)^2-21(45)-45=92,160 \end{gathered}`

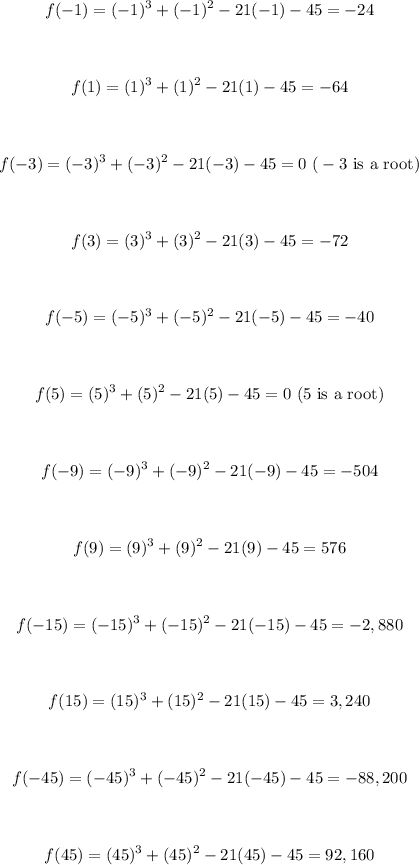
The answer is:

`\begin{gathered} x=-3 \\ \\ x=5 \end{gathered}`