Question

Find two positive numbers whose difference is 12 and whose product is 693.

Answer 1

Let be "x" and "y" the two positive numbers mentioned in the exercise.

You need to remember the following definitions:

- A Difference is the result of a Subtraction.

- A Product is the result of a Multiplication.

In this case, you know that their Difference is 12 and their Product is 693. So you can set up this System of Equations:

`\begin{cases}x-y=12 \\ xy=693\end{cases}`

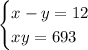
You can solve the System of Equation using the Substitution Method:

1. You can solve for the variable "x" from the first equation:

`x=12+y`

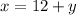
2. Substitute this new equation into the second original equation and simplify:

`\begin{gathered} xy=693 \\ (12+y)y=693 \\ y^2+12y=693 \end{gathered}`

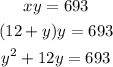
3. Now you have to solve for "y", in order to find its value:

- Rewrite the equation in this form:

`ax^2+bx+c=0`

Since it is the variable "y":

`ay^2+by+c=0`

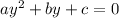
Then:

`y^2+12y-693=0`

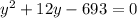
4. Use the Quadratic Formula to find the values of "y". The formula would be:

`y=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this case:

`\begin{gathered} a=1 \\ b=12 \\ c=-693 \end{gathered}`

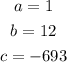
Then, substituting values and evaluating, you get:

`\begin{gathered} y=\frac{-12\pm\sqrt[]{(12)^2-(4)(1)(-693)}}{(2)(1)} \\ \\ y_1=-33 \\ y_2=21 \end{gathered}`

5. Since the numbers mentioned in the exercise are both positive, you must choose only the positive values. Therefore:

`y=21`

6. To find the value of "x", you have to substitute the value of "y" into the equation

`x=12+y`

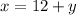
Then:

`x=12+(21)`

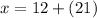
7. Finally, you have to solve the Addition:

`x=33`

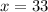
The answer is:

`33\text{ and }21`