Question

If a varies inversely as W^2, and z=20 when w=2, find z when w=3

Answer 1

Given:

z varies inversely as w²

so, we can write the following formula:

`z\propto(1)/(w^2)\rightarrow z=(k)/(w^2)`

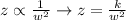
Where (k) is the constant of proportionality

We will find the value of (k) using the given data:

when z = 20, w = 2

so,

`\begin{gathered} 20=(k)/(2^2) \\ \\ k=20\cdot2^2=20\cdot4=80 \end{gathered}`

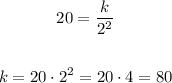
So, the equation will be as follows:

`z=(80)/(w^2)`

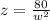
We will find the value of (z) when w = 3

so, substitute with w = 3

`\begin{gathered} z=(80)/(3^2) \\ \\ z=(80)/(9) \end{gathered}`

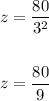
So, the answer will be z = 80/9