Question

Find the indicated function values for the function f(x) = 3x2 + 3x – 1.-a. f(0)b. f(2)c. f(-2)d. f(b)e. f(2a)

Answer 1

Given the function:

`f(x)=3x^2+3x-1_{}`

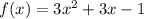
Let's find the following:

• (a). f(0)

To solve for f(0), substitue 0 for x and evaluate.

`\begin{gathered} f(0)=3(0)^2+3(0)-1^{} \\ \\ f(0)=3(0*0)+3(0)-1 \\ \\ f(0)=3(0)+3(0)-1 \\ \\ f(0)=0+0-1 \\ \\ f(0)=-1 \end{gathered}`

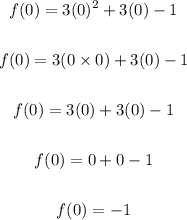
• b). f(2)

To solve for f(2), substitute 2 for x and evaluate:

`\begin{gathered} f(2)=3(2)^2+3(2)-1 \\ \\ f(2)=3(2*2)+3(2)-1 \\ \\ f(2)=3(4)+3(2)-1 \\ \\ f(2)=12+6-1 \\ \\ f(2)=18-1 \\ \\ f(2)=17 \end{gathered}`

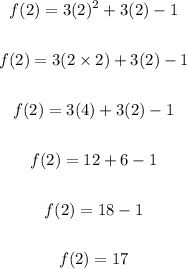
• (c). f(-2)

To solve for for f(-2), substitute -2 for x and evaluate:

`\begin{gathered} f(-2)=3(-2)^2+3(-2)-1 \\ \\ f(-2)=3(4)-6-1 \\ \\ f(-2)=12-6-1 \\ \\ f(-2)=5 \end{gathered}`

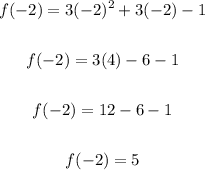
• d). f(b)

To solve for f(b) substitute b for x and evalaute:

`\begin{gathered} f(b)=3(b)^2+3(b)-1 \\ \\ f(b)=3(b* b)+3(b)-1 \\ \\ f(b)=3b^2+3b-1 \end{gathered}`

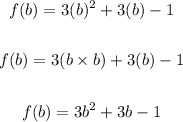
• e). f(2a)

Substitute 2a for x:

`\begin{gathered} f(2a)=3(2a)^2+3(2a)-1 \\ \\ f(2a)=3(2a*2a)+3(2a)-1 \\ \\ f(2a)=3(4a^2)+3(2a)-1 \\ \\ f(2a)=12a^2+6a-1 \end{gathered}`

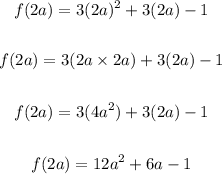
ANSWER:

a. f(0) = -1

b. f(2) = 17

c. f(-2) = 5

d. f(b) = 3b² + 3b - 1

e. f(2a) = 12a² + 6a - 1