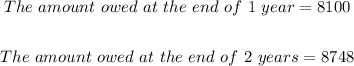Question

Suppose Lena borrows $7500 at an interest rate of 8%

Answer 1

Step-by-step explanation:

Given;

We are given a loan in the sum of $7,500 at the annual rate of 8% compounded yearly.

Required;

Calculate the amount owed at the end of 1 year. Also calculate the amount owed at the end of 2 years.

Step-by-step solution;

To calculate interest on a principal amount with the annual rate given, we shall use the following formula;

`A=P(1+r)^n`

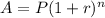
Where the variables are;

`\begin{gathered} A=Amount\text{ }owing\text{ }after\text{ }the\text{ }given\text{ }period \\ P=Principal\text{ }or\text{ }initial\text{ }amount \\ r=rate\text{ }of\text{ }interest\text{ }as\text{ }a\text{ }decimal \\ n=time\text{ }period(in\text{ }years) \end{gathered}`

Note that the rate will be expressed as decimal for this calculation. Hence, we will have;

`8\%=(8)/(100)=0.08`

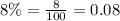
We can now apply the formula as follows;

`\begin{gathered} A=7500(1+0.08)^1 \\ \\ A=7500(1.08) \\ \\ A=8100 \end{gathered}`

Also at the end of two years, that is, when n = 2;

`\begin{gathered} A=7500(1+0.08)^2 \\ \\ A=7500(1.08)^2 \\ \\ A=7500*1.1664 \\ \\ A=8748 \end{gathered}`

Therefore, the amount owed on this loan at the end of each period are as follows;

ANSWER:

`\begin{gathered} The\text{ }amount\text{ }owed\text{ }at\text{ }the\text{ }end\text{ }of\text{ }1\text{ }year=8100 \\ \\ The\text{ }amount\text{ }owed\text{ }at\text{ }the\text{ }end\text{ }of\text{ }2\text{ }years=8748 \end{gathered}`