Question

There are five parts to this problem. The amount left after 10 seconds is blank grams.

Answer 1

ANSWERS

• After ,10, seconds: ,88 grams

,

• After ,20, seconds: ,44 grams

,

• After ,30, seconds: ,22 grams

,

• After ,40, seconds: ,11 grams

,

• After ,50, seconds: ,5.5 grams

Step-by-step explanation

The amount of substance remaining is,

`N(t)=N_o\left((1)/(2)\right)^(t/h)`

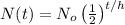
Where N₀ is the initial quantity of the substance, h is the half-life of the substance, t is the time and N(t) is the quantity remaining.

In this case, the initial quantity, N₀, is 176 grams and the half-life, h, is 10 seconds, so we have the formula,

`N(t)=176\left((1)/(2)\right)^(t/10)`

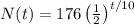
And we have to find N(10), N(20), N(30), N(40), and N(50):

`N(10)=176\left((1)/(2)\right)^(10/10)=176\cdot(1)/(2)=88`
`N(20)=176\left((1)/(2)\right)^(20/10)=176\cdot(1)/(2^2)=176\cdot(1)/(4)=44`
`N(30)=176\left((1)/(2)\right)^(30/10)=176\cdot(1)/(2^3)=176\cdot(1)/(8)=22`
`N(40)=176\left((1)/(2)\right)^(40/10)=176\cdot(1)/(2^4)=176\cdot(1)/(16)=11`
`N(50)=176\left((1)/(2)\right)^(50/10)=176\cdot(1)/(2^5)=176\cdot(1)/(32)=5.5`

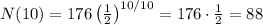
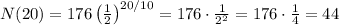
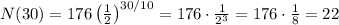
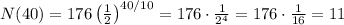
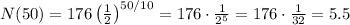
Hence, the amount of substance remaining after each period of time is:

• 10, seconds: ,88 grams

,

• 20, seconds: ,44 grams

,

• 30, seconds: ,22 grams

,

• 40, seconds: ,11 grams

,

• 50, seconds: ,5.5 grams