Question

Use the Quotient Property to Simplify Square Roots Number 129

Answer 1

Using the quotient property we would have

`\begin{gathered} \sqrt{(75r^9)/(8^8)}=(√(75r^9))/(√(8^8)) \\ \end{gathered}`

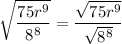
This follows the rule

`\sqrt{(a)/(b)}=(√(a))/(√(b))`

From the simplified expression as shown above

`(√(75r^9))/(√(8^8))=(√(3*25* r^9))/(√((2^3)^8))`

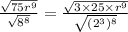
Thus;

`(√(3*25r^9))/(√((2^3)^8))=\frac{√(25)*√(3)*√(r^9)}{\sqrt{2^(^3*8)}}=\frac{5√(3r^9)}{\sqrt{2^(24)}}`

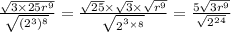
Therefore

`\begin{gathered} Using\text{ fraction index law we could simplify the denominator} \\ \frac{5√(3r^9)}{2^{(24)/(2)}}=(5√(3r^9))/(2^(12)) \end{gathered}`

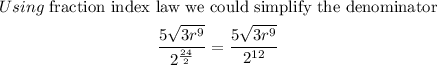
We can not simplify the 3 and the r raised to power of 9 as their power is not even, hence the final answer is given below

`(5√(3r^9))/(2^(12))=(5√(3r^9))/(4096)`

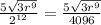
The final answer is :

`(5√(3r^9))/(4096)`