Question

Find the x-intercept and y-intercept of the graph of 2x+6y=6 . Then graph.x-intercept = (,0)y-intercept = (0,)12345-1-2-3-4-512345-1-2-3-4-5Clear All Draw: LineParabolaAbsolute valueCircleDotQuestion HelpQuestion 2: Video1

Answer 1

Step 1:

In this question, we are meant to find the x-intercept and y-intercept of the graph of :

`\text{2x + 6y = 6}`

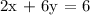
First, we are meant to graph it

Second, we are meant to find:

a) x-intercept

b) y - intercept

Step 2:

The graph of :

`\text{2 x + 6y = 6}`

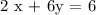
is as follows:

Step 3:

Given the equation:

`\begin{gathered} 2x\text{ + 6y = 6} \\ For\text{ the x-intercept, we have that:} \\ \text{when y = 0, we have that:} \\ 2x\text{ + 6 (0 ) = 6} \\ 2\text{ x+ 0 = 6} \\ 2x\text{ = 6} \\ \text{Divide both sides by 2 , we have that:} \\ \text{x = }(6)/(2) \\ \text{x = 3} \\ \text{Then , the x - intercept = ( 3, 0 )} \end{gathered}`

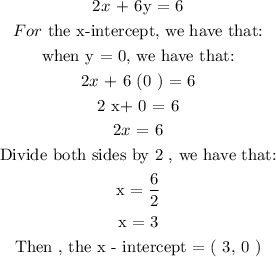
Next, given the equation:

`\begin{gathered} 2x\text{ + 6 y = 6} \\ For\text{ the y - intercept, we have that:} \\ \text{when x = 0 , we have that:} \\ 2\text{ ( 0 ) + 6 y = 6} \\ 0\text{ + 6y = 6} \\ 6y\text{ = 6} \\ \text{Divide both sides by 6, we have that:} \\ y\text{ = }(6)/(6) \\ y\text{ = 1} \\ \text{Then , the y -intercept = ( 0 , 1 )} \end{gathered}`