1)First, lets arrange our data in ascending order:
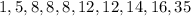
notice that we have the following:
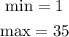
now, since we have ten elements in your data set, we can find the median by adding the two central elements. In this case we have:
![\begin{gathered} \operatorname{median}=(8+12)/(2)=(20)/(2)=10 \\ \operatorname{median}=10 \end{gathered}]()
Next, notice that we can divide our data set in two equal parts:
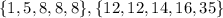
the median in these two subsets are going to be or first and third quartile, therefore, we have that:
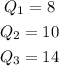
Now we can find the IQR:
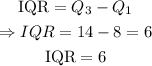
Finally, the outliers are the following for 1.5 interquantile:
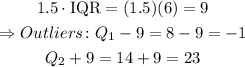
2)The box and whisker plot would be the following:
3)We can find the mean with the following formula:
![\operatorname{mean}=(\sum ^n_(i=1)x_i)/(n)]()
In this case, the mean is:
![\begin{gathered} \operatorname{mean}=(1+5+8+8+8+12+12+14+16+35)/(10)=(119)/(10)=11.9 \\ \operatorname{mean}=11.9 \end{gathered}]()
therefore, the average life span is 11.9
$)We can find the mean absolute deviation (or MAD), with the following expression:
![\text{MAD}=\frac{\sum ^{}_{}|x_i-\operatorname{mean}|}{n}]()
with this expression we can find out the variability of the dataset.
In this case, we have the following:
![\begin{gathered} \text{MAD}=(|1-11.9|+|5-11.9|+|8-11.9|+|8-11.9|+|8-11.9|+|12-11.9|+|12-11.9|+|14-11.9|+|16-11.9|+|35-11.9)/(10) \\ =(10.9+6.9+3.9+3.9+3.9+0.1+0.1+2.1+4.1+23.1)/(10) \\ =(59)/(10)=5.9 \\ \text{MAD}=5.9 \end{gathered}]()
We have that the MAD for the average lifespan is 5.9
5) Since the mean absolute deviation is 5.9, we can estimate that the values of the dataset are approximately 5.9 units away from the mean. therefore, there is a high variability in the life span of the animals