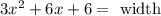We know that the area of a rectangle is the width multiplied by its length, basically
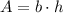
But here, we have the area, which is a polynomial, same for the length, then, to find out the width we must do a division of polynomial, I'll call the unknown polynomial as P, we have
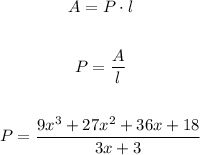
So now we got to solve
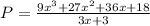
There is a lot of ways to solve it, first, I'll factor 3 in the denominator
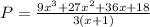
As well the numerator
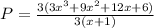
Then we can already simplify 3, and get an easier expression
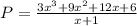
Now I'll factor using the grouping method, I want the numerator to be something like (x+1)*(another polynomial), doing that we can "cut" the (x+1).
One way to do it is to expand it in some simple sums, look at 3x³, we want a 3x² to match with him, but look that 9x² is 3x²+6x², let's write that way
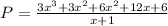
It doesn't seem to help us at all, but look that now we can factor 3x², then

Look, we have our first (x+1) in the numerator. Let's use the same idea but now for the term 6x², we want a 6x to match with him, we have 12x, so let's write it as 6x + 6x.

Similar to what we did before, factor 6x, and again
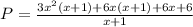
Now we have one more (x+1).
Now the easiest one, factor 6
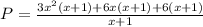
As we can see we have (x+1) multiplied by something in all terms in the numerator, then we can factor (x+1) now
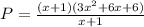
Now we can cancel (x+1), and our final expression will be
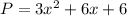
Therefore, the width is