Question

Suppose median family income is normally distributed with mean M = $44000 and standard deviation O = $15000. Let 2 represent median family income. What is the probability that for a family chosen at random 2' lies between $29600 and $ 30500?

Answer 1

First, let's calculate the critical value z for each of the given end values of the interval, that is, 29600 and 30500.

To do so, we can use the formula below:

`\begin{gathered} z=(x-\mu)/(\sigma)\\ \\ z_1=(29600-44000)/(15000)=-(14400)/(15000)=-0.96\\ \\ z_2=(30500-44000)/(15000)=-(13500)/(15000)=-0.9 \end{gathered}`

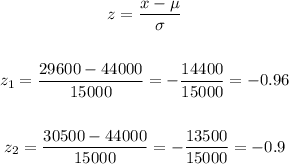
Now, we need to find the probabilities associated to each of these critical values.

Looking at the z-table, for z = -0.96 we have p = 0.1685 and for z = -0.9 we have p = 0.1841.

Since we want the values inside this interval, let's calculate the difference of the probabilities:

`p=0.1841-0.1685=0.0156`

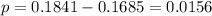
Therefore the probability is 0.0156.