Question

Type in the value ol 29 С A 21 20 B sin A= COSA = tanA= sinC = cosC =

Answer 1

Given,

The measure of side AC is 29.

The measure of side AB is 20.

The measure of side BC is 21.

The angle ABC is right angle.

The expression of sin in trigonometric ratio is,

`\begin{gathered} \sin \text{ A=}\frac{\text{side opposite to angle A}}{\text{Hypotenuse}} \\ \sin \text{ A=}(21)/(29) \\ \sin \text{ C=}\frac{\text{side opposite to angle C}}{\text{Hypotenuse}} \\ \sin \text{ C=}(20)/(29) \end{gathered}`

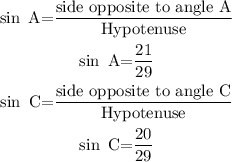
The expression of cos in trigonometric ratio is,

`\begin{gathered} \cos \text{ A=}\frac{\text{side adjacent to angle A}}{\text{Hypotenuse}} \\ \cos \text{ A=}(20)/(29) \\ \cos \text{ C=}\frac{\text{side adjacent to angle C}}{\text{Hypotenuse}} \\ \cos \text{ C=}(21)/(29) \end{gathered}`

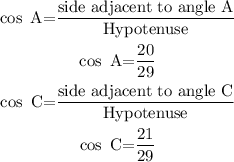
The expression of tan in trigonometric ratio is,

`\begin{gathered} \tan \text{ A=}\frac{\text{side opposite to angle A}}{\text{side adjacent to angle A}} \\ \tan \text{ A=}(21)/(20) \\ \tan \text{ C=}\frac{\text{side opposite to angle C}}{\text{side adjacent to angle C}} \\ \tan \text{ C=}(20)/(21) \end{gathered}`

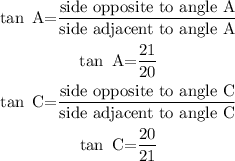
Hence, the value of sin A is 21/29, cos A is 20/29 , tan A is 21/20 and the value of