Question

For the following exercise determine whether the graph shown represents a geometric sequence.

Answer 1

Graph of a geometric sequence

equal changes in the input cause the output to be successively multiplied by a constant. cause the output to be successively multiplied by a constant (determined by the common ratio). Thus, geometric sequences always graph as points along the graph of an exponential function.

An example of a geometric sequence is given below as

A geometric sequence takes the function given in the formula below

`a_n=ar^(n-1)`

When n=1, An=-3

`\begin{gathered} a_(n)=ar^(n-1) \\ -3=ar^(1-1) \\ -3=a \\ a=-3 \end{gathered}`

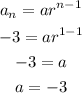
When n=2 ,An=-1

`\begin{gathered} a_(n)=ar^(n-1) \\ -1=-3r^(2-1) \\ -1=-3r \\ r=(-1)/(-3) \\ r=(1)/(3) \end{gathered}`

When n=3,An =1

`\begin{gathered} a_(n)=ar^(n-1) \\ 1=3r^(3-1) \\ (1)/(3)=r^2 \\ r^=\sqrt{(1)/(3)} \end{gathered}`

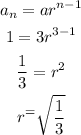
We can see that they do not have a constant value of the common ratio (r)

Hence,

The graph DOES NOT represent a geometric sequence