Question

Use the graph at the top of the page for 22 and 23. A) 8/3 B) 8 C) - 1/8 D) -3/8 22) Write the slope of the line that would be parallel to h(x)23) Write the slope of the line that would be perpendicular to h(x)

Answer 1

Given the line h(x), it can be observed that two points with coordinate below can be located

`\begin{gathered} (-4,0),\text{point where h(x) cut the x-axis} \\ (4,-1),\text{point where h(x) and m(x) cross each other} \end{gathered}`

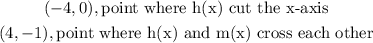
The slope,s, of a line given coordinates of two points can be found using the formula below:

`\begin{gathered} s=(y_2-y_1)/(x_2-x_1) \\ \text{points} \\ (x_1,y_1),(x_2,y_2) \end{gathered}`

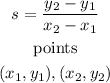
The slope of the line h(x) with the coordinates of the two points gotten can be gotten as shown below

`\begin{gathered} (-4,0),(4,-1) \\ s_(h(x))=(-1-0)/(4--4) \\ s_(h(x))=(-1)/(4+4) \\ s_(h(x))=-(1)/(8) \end{gathered}`

It should be noted that two parallel lines have the same slope, while the slope of two perpendicular lines can be found to be negative inverse of their slopes

For example, if m1 is the slope of a line, the slope of its parallel line would be m1. But the slope of the perpendicular line would be -1/m1

The slope of the line that would be parallel to h(x) is the same as the slope of h(x)

The slope of the line that would be perpendicular to h(x) would be negative inverse of the slope of line h(x)

`\begin{gathered} s_{\text{parallel}}=-(1)/(8) \\ s_{\text{perpendicular}}=(-1)/(-(1)/(8))=-1*(-8)/(1)=8 \end{gathered}`

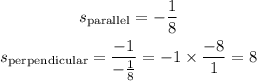
Hence, The slope of the line that would be parallel to h(x) is -1/8, while the slope of the line that would be perpendicular to h(x) is 8