Question

I need to find the volume and surface area of this 3d composite figure

Answer 1

Volume:

To find the volume we notice that this figure is made of a cube minus a cone.

The volume of a cube is given as:

`V=l^3`

Here the length of each side is 6 cm.

The volume of a cone is given as:

`V=(1)/(3)h\pi r^2`

here the radius of the cone is 2 cm (half the diameter shown) and its height is 6 cm.

Hence the volume of the composite figure is:

`V=(6)^3-(1)/(3)(6)\pi(2)^2=190.87`

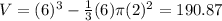
Surface area:

The surface area of the figure is the surface area of the cube minus the surface area of the cone.

The surface area of the cube is given by:

`SA=6l^2`

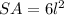
in this case the lenght of each side is 6 cm.

The surface area of the cone is given by:

`SA=\pi r^2+\pi rl`

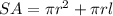
where r is the radius of the cone and l is the slant height. The radius of the cone is 2 cm. To find the slant height we need to remember that this slant height is the hypotenuse of a right triangle with one leg equal to the radius and the other leg equal to the height of the cone. Then, using the pythagorean theorem we have:

`\begin{gathered} l^2=2^2+6^2 \\ l^2=4+36 \\ l=\sqrt[]{40} \end{gathered}`

Once we have all the values we need we have that the surface area is:

`SA=6(6)^2-\pi(2)^2-\pi(2)(\sqrt[]{40)}=163.70`

Summing up we have that:

• The volume is 190.87 cubic cm.

,

• The surface area is 163.70 squared cm.