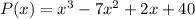The zeros of the equation is given below as
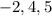
Step 1:
Express the zeros as factors of the polynomial P(x), we will have
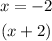
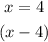
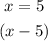
Step 2:
Multiply the first two factors by expanding them
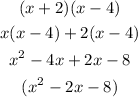
Step 3 :
Multiply the expression gotten in step 2 by (x-5) from step 1
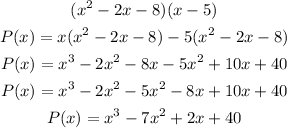
Therefore,
The final answer is