the length of the shorter leg = 10m
Step-by-step explanation:
longer leg = 24m
shorter leg = ?
hypotenuse = 6 more than twice the shorter leg
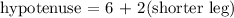
Since the triangle is a right angled triangle, to get the shorter leg we will apply pythagoras theorem:
Hypotenuse² = opposite² + adjacent²
Hypotenuse² = (shorter leg)² + (longer leg)²
substitute the values in the formula:
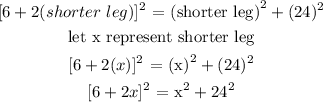
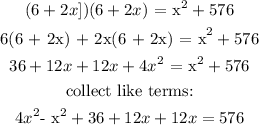
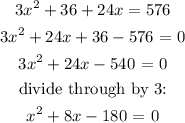
To get x, we will apply factorisation method:
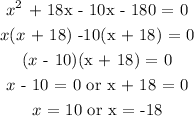
Since we can't have a negative length, the value of x will be 10
As a result, the length of the shorter leg = 10m