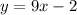To answer this question, we need to remember that the slope-intercept form of the line is of the form:

Where:
1. m is the slope of the line, and
2. b is the y-intercept of the line (that is the point when x = 0).
Then, we have from the question that:
m = 9
And the point is (1, 7).
Therefore, using the point-slope form of the line, we can proceed as follows to find, finally, the slope-intercept form of that line:

x1 = 1
y1 = 7

Then, add 7 to both sides of the equation to solve for y:
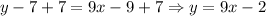
Therefore, the equation of the line in slope-intercept form is: