Question

Find the quadratic equation using the points given (-2,1) (-1,0) and (1,4)

Answer 1

We have 3 points and we have to find the quadratic equation.

One of the points is a zero: (-1,0).

Then, we can write:

`f(x)=a(x+1)(x+b)`

We have 2 parameters to find.

We can expand the function and then solve the system of equations:

`\begin{gathered} f(x)=a(x+1)(x+b) \\ f(x)=a(x^2+bx+x+b) \\ f(x)=a(x^2+x+b(x+1)) \end{gathered}`

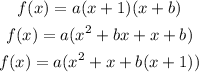
For point (-2,1) we will replace x and y and get:

`\begin{gathered} 1=a((-2)^2+(-2)+b(-2+1)) \\ 1=a(4-2+(-1)b) \\ 1=a(2-b) \\ a=(1)/(2-b) \end{gathered}`

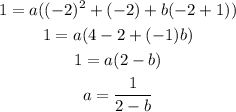
For point (1,4) we replace for x, y and also a:

`\begin{gathered} 4=(1)/(2-b)(1^2+1+b(1+1)) \\ 4=(1)/(2-b)(2+2b) \\ 4(2-b)=2+2b \\ 8-4b=2+2b \\ 8-2=2b+4b \\ 6=6b \\ b=1 \end{gathered}`

Then, we can calculate for a:

`a=(1)/(2-b)=(1)/(2-1)=(1)/(1)=1`

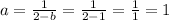
Then, we can replace a and b in the equation and expand:

`\begin{gathered} f(x)=1(x+1)(x+1) \\ f(x)=x^2+2x+1 \end{gathered}`

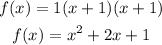
We can test with a graph if the equation fit the points given:

Answer: f(x) = (x+1)^2 = x^2+2x+1