Given:
![h(x)=\frac{6\sqrt[]{4x+3}}{9x-4}](https://img.qammunity.org/2023/formulas/mathematics/college/idjlghwbpsu8mz9uf2krimqc64hblhkscg.png)
a) The domain of the function is a set of all input values for which the function is real and defined.
First, find the on-negative values of radical and undefined points.
![\begin{gathered} 4x+3\ge0\ldots\text{.non}-\text{negative values for radical} \\ 4x\ge-3 \\ x\ge-(3)/(4) \\ \text{the function is undefined when 9x-4=0} \\ 9x-4=0 \\ 9x=4 \\ x=(4)/(9) \end{gathered}]()
The domain is,
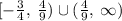
b) Range of the function is a set of dependant variables for which the function is defined.
The range is,
![-\infty<strong>Answer:</strong>[tex]\text{Domain:}\lbrack-(3)/(4),\: (4)/(9))\cup((4)/(9),\: \infty)](https://img.qammunity.org/2023/formulas/mathematics/college/8itk8a5hvrfa6d47cl3gghm93252kynwx0.png)