Since angleCDE is equal to x and angleEDF is 3x+20, we have
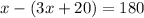
Now, by distributing the minus sign into the parenthesis (Distributive property) we have
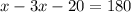
By combining similar terms (Addition property), we get

By adding 20 to both sides (Inverse property of addition), we obtain

Finally, by multiplying both side by -1/2 (Inverse property of Multiplication), we get
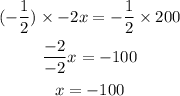
Then, x is equal to -100