ANSWERS
(a) 2 m³
(b) 2.86 kg
Step-by-step explanation
(a) The ideal gas equation is,
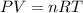
Where P is the pressure of the gas, V is the volume it occupies, T is the temperature, n is the number of moles of gas in the sample and R is the universal gas constant.
We want to find the volume of a sample of oxygen if the temperature and pressure are changed. This means that we will have the same number of moles of gas, n and, since R is a constant, the product nR is constant,
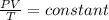
In this case, the initial state of the gas is P₁ = 752 mmHg, V₁ = 2.17 m³, T₁ = 20°C. We have to find the volume V₂ when P₂ = 760 mmHg and T₂ = 0°C. Use the relationship,
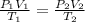
Note that the temperature must be in Kelvin, not degrees Celsius. For that, add 273.15 to each temperature,
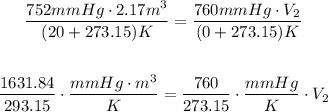
Solving for V₂,
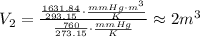
Hence, the volume of the same sample of oxygen at standard temperature and pressure is 2 m³.
(b) To find the mass of oxygen, we have to use the density of that gas,
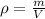
We know that the density ρ = 1.43 kg/m³ and that the volume at standard temperature and pressure is 2m³. Solve the equation above for m,
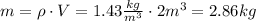
Hence, there are 2.86 kilograms of oxygen in the sample.