Question

20.A card is drawn from a standard deck of 52 cards, and then replaced in the deck. Find the probability that at least one king is drawn by the fourth draw. Round your answer to two decimal places. Do not round until your final calculation.

Answer 1

In order to find the probability of at least one king being drawn, let's calculate the probability of the complementary event, that is, no king being drawn.

There are 4 kings in a 52 cards deck, so the probability of drawing a king is 4/52 and not drawing a king is 48/52.

The probability of drawing 4 cards (with replacement) and none of them being a king is:

`P(no\text{ }king\text{ x4})=((48)/(52))^4`

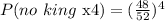
Then, the probability of drawing 4 cards (with replacement) and at least one of them being a king is:

`\begin{gathered} P(\text{at least one king})=1-P(no\text{ }king\text{ x4})\\ \\ =1-((48)/(52))^4=0.2740 \end{gathered}`

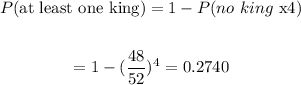
Rounding to the nearest hundredth, the probability is 0.27.